Simulation 有限元分析实战（1）：理解圣维南原理

2026年1月18日 21:29:10ZDJ

ZDJ

管理员

关注

1469
文章

0
粉丝

Simulation评论20字数 2870阅读模式

一、问题描述：

本案例的目的是确定下图所示的往复式凸轮从动件中的应力。具体而言，需要确定的应力是在凸轮从动件上端附近、穿过机架支撑处的圈出区域内的应力。

下图展示了凸轮从动件上的具体尺寸和施加的载荷。凸轮在X方向和Y方向上对从动件施加的分力分别为Fx=-1636.95N和Fy=4492.7N，这些力作用在从动件底部的滚销上。由于要进行静态应力分析，凸轮从动件的上端被视为“固定端”，上端支撑处显示了相应的反作用力Rx、Ry。

二、分析步骤：

1.下载配套模型并打开，模型如下图所示。

2.点击【新算例】，在【名称】中输入“凸轮从动件线性静应力分析 1”，【类型】选择“静应力分析”，如下图所示。

3.为模型指定材料属性。

1）右键单击Cam Follower，然后从下拉菜单中选择“应用/编辑材料”，如下图所示。

此时会打开“材料”窗口，如下图所示。在“材料”窗口的左侧栏中，选择“AISI 1045 钢，冷拔”，随即该材料的属性会显示在表格的右半部分。

2）将单位改成MPa，可以看到该材料的屈服强度为530MPa，单击应用按钮。

3）在“仿真管理器”树中，Cam Follower图标上现在会出现一个绿色的勾号，表示材料属性已定义，并且零件名称旁边会列出（-AISI 1045 钢，冷拔-）。

4.施加约束。

在本分析中，模型的顶面，即凸轮从动件进入框架的位置，被假定为“固定”状态。这种约束与凸轮从动件的情况相符，该从动件的上端位于框架中一个接近零间隙的槽内，且此处假定进行静态分析。

1）在仿真管理器中，鼠标右键单击“夹具”，然后从下拉菜单中选择“固定几何体”，如下图所示。

2）此时会出现如下图所示的“约束”属性管理器，点击属性管理器中的“固定几何体”图标，然后选择模型的上端面，此选项将该面的X、Y和Z方向的平移自由度均设置为零，点击勾号完成。

对于实体模型（如凸轮从动件），施加固定约束会阻止端面在X、Y和Z方向上的平移。这种类型的约束被称为“不可移动”约束，因为它仅限制模型上所选每个节点的三个自由度。当固定约束应用于壳单元或梁单元时，不仅会阻止节点在X、Y和Z方向上的平移自由度，还会限制每个受约束节点绕X、Y和Z轴的旋转自由度。

5.应用外部载荷。

1）在仿真管理器中，鼠标右键单击“外部载荷”，然后从下拉菜单中选择“力”，如下图所示。

2）在“力/扭矩”属性管理器的“类型”选项卡下，点击“力”，选择模型底部端面的分割线（蓝色），然后勾选“选定的方向”，选择模型的竖直边（粉红色），设置单位为SI，力值为4492.7N，如下图所示。

3）再次在分割线上施加一个水平的力。操作步骤如上，区别是选定的方向选择模型底部的水平直线，力值为1636.95N，力的方向为水平指向左侧，如下图所示。

完成后的外部载荷如下图所示。

由于我们需要研究凸轮从动件上端的应力，因此在模型下端中心（即滚子与从动件相连的位置）施加力载荷这一简化假设可能被认为是可接受的。如果分析的重点是确定模型其他位置的应力，那么为什么要花费大量时间和精力去模拟滚子销与凸轮从动件之间的接触应力呢？另一方面，如果本分析的重点是研究连接滚子和凸轮从动件的销附近的应力，那么该几何结构的细节就必须包含在模型中。

6.网格划分。

1）在Simulation管理器中，右键单击“网格”图标，然后从下拉菜单中选择“生成网格”，如下图所示。

2）会打开如下图所示的“网格”属性管理器。在网格参数中勾选”标准网格“，我们可以看到当前网格参数。

3）单击确定以接受默认值，此时网格划分会自动开始。网格划分完成后，Simulation会显示已划分网格的模型，如下图所示。此外，Simulation管理器树中的“网格”图标上会出现一个绿色勾号，表示网格划分已完成。

7.运行分析。

1）鼠标右键单击位于“仿真”管理器树顶部的Cam Follower ，从下拉菜单中选择“运行”，求解过程将自动开始。

2）静态分析成功求解后，会在“仿真”管理器树的底部创建一个名为“结果”的新文件夹。该文件夹包含3个子文件夹，包含当前模型分析产生的默认图表。

8.结果后处理。

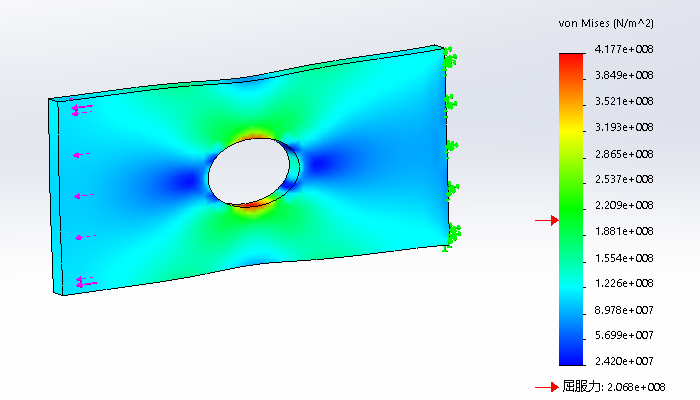
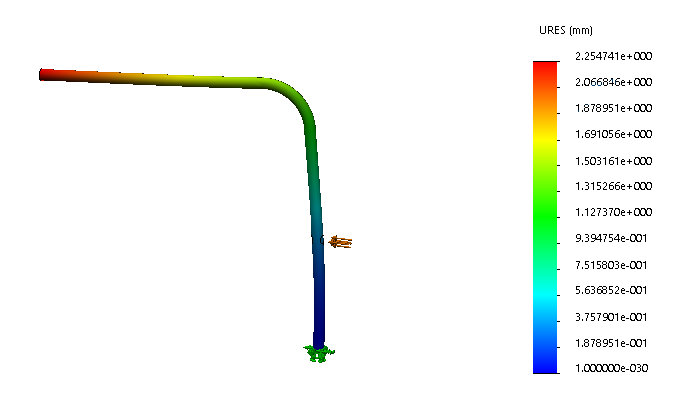
1）双击应力1（-vonMises-）图表，此时我们可以看到最大的vonMises应力为451.1MPa，小于材料的屈服强度530MPa。

2）双击位移1（-合位移-）图表，此时我们可以看到最大变形量为为0.325mm。

三、结果对比

1.应力公式计算结果

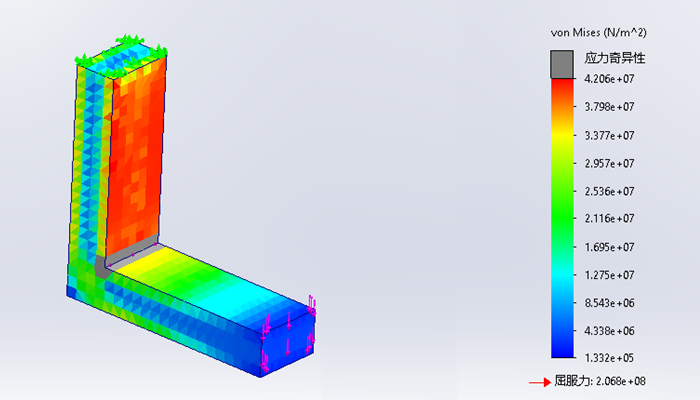
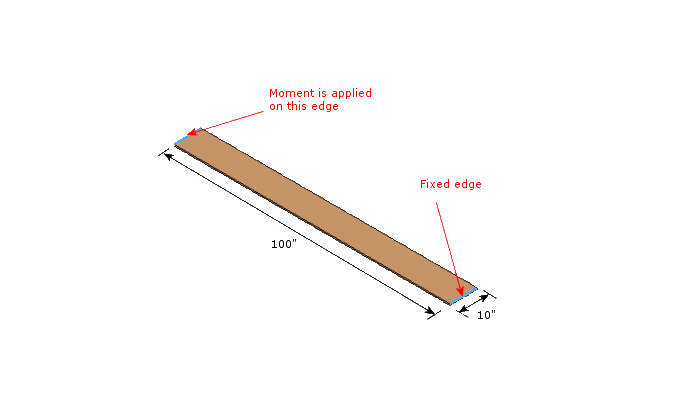
如下图所示，凸轮从动件的下端受到X和Y两个方向的力分量，向上作用的力分量Fy=4492.7N，在Y方向产生轴向压应力，其计算公式为σ=F/A。尽管该应力显示在凸轮从动件的下端附近，但经典应力方程假定它在整个模型中从上到下均匀分布。

同样，垂直于凸轮从动件长度方向作用的力的X分量Fx=1636.95N会产生弯曲应力，如图中模型顶部所示，其计算公式为σ=Mc/I。由于Fx作用在凸轮从动件的底部，力臂长度最大（127.0mm），所以弯曲应力在模型顶部达到最大值。凸轮从动件的宽度为25.4mm，厚度为12.7mm。

由于图中所示的所有应力都沿Y方向作用，因此只要包含正确的正负号，就可以通过简单地将轴向应力和弯曲应力的大小相加来组合它们。

A点的应力因轴向应力和弯曲应力而处于受压状态，因此：

A点的应力：σ = σ轴向 + σ弯曲 = (-13.93) + (-152.24) = -166.17 MPa。

B点的应力因轴向应力而处于受压状态，但中性轴上的弯曲应力为零，因此：

B点的应力：σ = σ轴向 + σ弯曲 = (-13.93) + (0) = -13.93 MPa。

C点因轴向应力而处于受压状态，但因弯曲应力而处于受拉状态。由于“+”号的拉伸弯曲应力大于“-”号的压缩轴向应力，C点的合成应力为：

C点的应力：σ = σ轴向 + σ弯曲 = (-13.93) + (+152.24) = +138.31 MPa。

2.应力仿真计算结果

接下来，将上述结果与通过有限元仿真分析得到的结果进行比较。为此，需要绘制Y方向的法向应力分布图。操作步骤如下：

1. 在模拟管理器中，鼠标右键单击“结果”文件夹，然后从下拉菜单中选择“定义应力图解”，如下图所示。

此时会打开“应力图”属性管理器，如下所示。在定义选项卡中的“显示”对话框中，从下拉菜单中选择SY：Y方向法向应力。这与之前通过公式计算得到的应力是相同的。为方便查看模型内部的应力，勾选“'真实比例”，以按真实大小显示模型的变形。

2.在设定选项卡中的“边缘选项”对话框中，从下拉菜单中选择“离散”，然后将边界选项设置为“网格”，此选项会用黑线勾勒模型边缘，从而使其边缘更易于查看。

3.点击勾号完成，此时我们可以看到如下图所示的结果。

现在我们准备将计算的应力与通过有限元仿真分析得到的应力值进行比较。

4. 由于要检查Y方向的应力，在Simulation管理器树中，右键单击上一步创建的“应力2（-Y正交-）”，然后从下拉菜单中选择探测，“探测结果”属性管理器的部分视图会打开。

5.在“选项”对话框中，选择“在所选实体上”。

然后点击凸轮从动件顶部前边缘上的线，最后点击【更新】按钮。此操作会将数据填充到结果表格中，表格中的数据如下图所示。

6.找到下图所示的三个位置的应力值。

7.下表对比了在凸轮从动件顶端的A、B、C位置处，手动计算的应力结果与使用探测工具获得的有限元结果。

上表中的结果表明：使用应力方程计算的结果与使用有限元仿真分析方法的结果之间存在显著差异。这是为什么呢？通过回顾圣维南原理可以回答上述问题，该原理指出，经典方程所预测的应力仅存在于远离以下位置的区域：（1）载荷施加位置（2）支撑位置（3）几何不连续位置。这些情况中的任何一种通常都会产生显著的局部效应。因此在这些区域，应力方程的局限性与有限元方法所得到的结果不一致。出于这个原因，再次使用探测工具，但这次选择离模型上部支撑位置稍远的节点处。

8.将探针工具移至图形区域，然后向下数到左上角下方的4节点。该节点被随意假定为与施加在凸轮从动件顶部的固定约束条件“足够远”。选择这个位置是为了减小圣维南原理所预测的影响。

从左到右在模型上移动，点击选择仅位于单元角点的节点，如下图中的小圆所示。